467C: George and Job ⧉

A variation on the Knapsack problem. To state the problem in knapsack terms, you can fit k items in your bag. Optimize the sum of their values. The twist is the items are actual m-length segments of an array of values. This means if you choose the ith item to put in your bag, you can't choose the i+pth segments for p in {1,2,...,m-1}. Basically choosing one segment excludes choosing all overlapping segments.

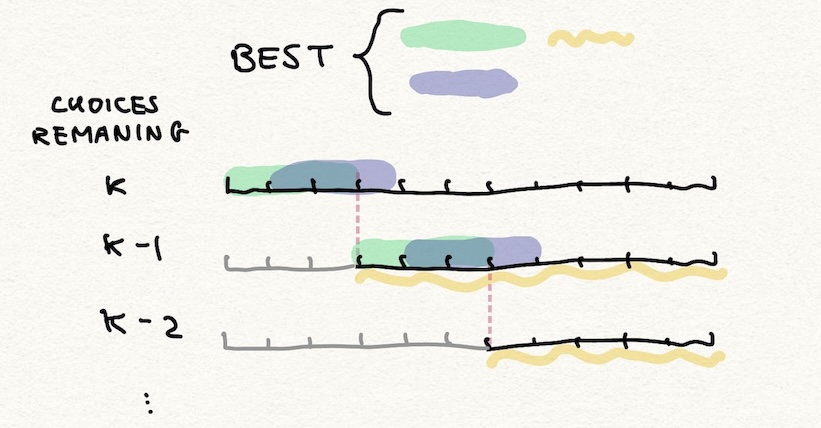
We can solve this problem using dynamic programming. The key observation, which I'll credit to my friend Hoang for helping me see, is this: For some start in [0, number of segments] and remaining in [0, number of choices], the best remainingth choice for a segment from the range [start, number of segments] is either ...

... the segment at start PLUS the best remaining - 1th choice for a segment from the range [start + segment width, number of segments], OR
... the best remainingth choice for a segment from the range [start + 1, number of segments]

In the picture below, the green blob is the segment at start, the blue blob is the segment at start + 1, and the yellow squiggle represents the bounds of the subproblem when we choose the green blob and recursively solve from start + m, remaining - 1.

An illustration of the bullet points above

Considering these two options for each start and remaining constitutes a recursive strategy for solving the problem. The dynamic programming step is to simply cache the optimal sum for each start and remaining in the problem's state-space.

We can preprocess the original array to get the sum of each segment in O(n). Caching results in a matrix dp[remaining][start] means we can recall solutions to subproblems in constant time. Therefore the complexity of this solution is O(number of segments * number of choices) or O((n-m+1) * k).

#include <iostream>
#include <functional>
#include <numeric>
#include <algorithm>
#include <array>
#include <vector>
using namespace std;
using ll = long long;
ll dp[5000][5000];
int main() {
	int n,m,k;
	cin >> n >> m >> k;
	vector<ll> a (n);
	for (auto& x : a) cin >> x;
	const int num_segments = n-m+1;
	for (int r = 0; r < k; ++r) {
		for (int c = 0; c < num_segments; ++c) {
			dp[r][c] = -1;
		}
	}
	// preprocessing -- precompute all m-length segment sums.
	// segment_from[i] = sum of m consecutive elements of a starting from i, a[i .. i+m-1]
	vector<ll> segment_from (num_segments, 0);
	ll running_sum = accumulate(a.begin(), a.begin()+m, 0LL);
	for (int i = 0; i < num_segments; ++i) {
		segment_from[i]=running_sum;
		running_sum -= a[i];
		running_sum += a[i+m];
	}
	// the optimal `i`th choice is either
	// ... the segment at `start` plus the optimal `i + 1`th choice
	//							~~ OR ~~
	// ... the optimal `i`th choice starting from `start + 1`
	function<ll(int,int)> pick_subseq = [&] (int start, int remaining) {
		if (start >= num_segments || remaining < 0) return 0LL;
		if (dp[remaining][start] != -1) return dp[remaining][start];
		ll alternative = pick_subseq(start+1, remaining);
		ll best_next = pick_subseq(start+m, remaining-1);
		dp[remaining][start] = max(alternative, segment_from[start] + best_next);
		return dp[remaining][start];
	};
	ll ans = pick_subseq(0, k-1);
	cout << ans << '\n';
	// thanks for helping me with this problem, Hoang!
}

If you found this solution helpful, consider leaving a star!