Abridged Reading ⧉

This problem stumped me in the ECNA 2021. I revisited the problem today with fresh eyes to see how my approach has changed over the last year. Pays to practice!

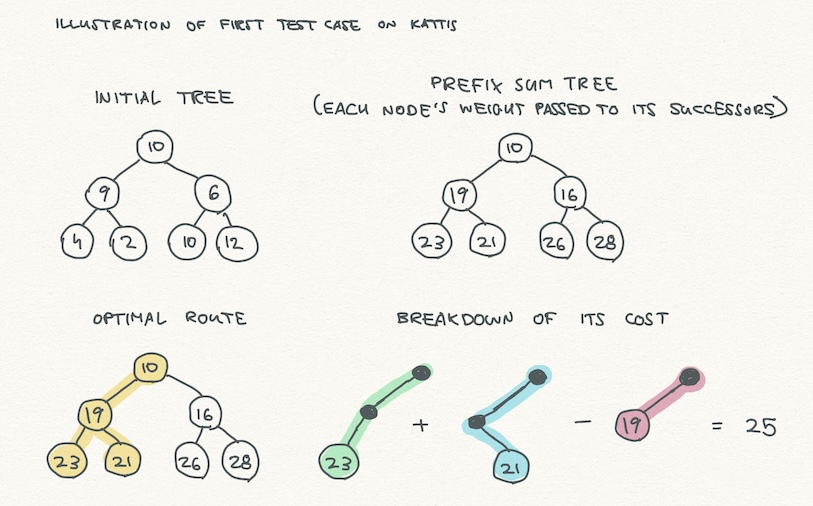
The problem describes a graph of dependencies between chapters in a book. Each chapter has a number of pages (its cost to read) and 0 or more chapters that must be read after it. If a chapter has no successors, then it is a "culminating concept" chapter. The task is to find the two "culminating concept" chapters that require the least total pages to read. The problem states that a chapter has at most one prerequisite. This means the chapters form a tree. The task can then be restated as "find the lowest-cost branching path in the tree that passes through the root(s) and two leaf nodes".

The main concept behind solving this problem is the lowest common ancestor (LCA). The lowest common ancestor of two nodes is the first "lowest" node in the tree that appears in both nodes' paths. Being as we don't need to reread a shared prerequisite between two chapters, if we count the root-to-node cost of two leaves, we can subtract the root-to-node cost of their LCA.

An illustration of our solution for the first test case on Kattis

With this in mind, the solution can be laid out in a few steps:

Connect the graph, taking note of nodes with no prerequisite (roots) and nodes with no successors (leaves).
Determine the root-to-node path cost and depth of each node with a DFS.
For each pair of leaves, see if their total cost minus the cost of their LCA, if any, is less than the current best.

#include <iostream>
#include <functional>
#include <vector>
using ll = long long;
using namespace std;
int main () {
  int n, m;
  cin >> n >> m;
  vector<vector<int>> adj (n);
  vector<ll> cost (n, 0),
             parent (n, -1),
             outdegree (n, 0),
             depth (n, 0),
             roots,
             leaves;
  // read costs  
  for (auto& c : cost) cin >> c;
  // connect tree
  for (int i = 0; i < m; ++i) {
    int from, to;
    cin >> from >> to;
    from--; to--;
    adj[from].push_back(to);
    parent[to] = from;
    outdegree[from]++;
  }
  // determine parents and leaves
  for (int i = 0; i < n; ++i) {
    if (parent[i]==-1) roots.push_back(i);
    if (outdegree[i]==0) leaves.push_back(i);
  }
  // pass down cost and depth through the tree
  // a "treefix sum", if you will...
  function<void(int)> pass_down_from = [&] (int parent) {
    for (auto child : adj[parent]) {
      cost[child] += cost[parent];
      depth[child] = depth[parent]+1;
      pass_down_from(child);
    }
  };
  for (auto root : roots) { pass_down_from(root); }
  
  // determine the cost of the lowest common ancestor of nodes a and b
  function<ll(int,int)> lca_cost = [&] (int a, int b) {
    while (depth[a] < depth[b]) { b = parent[b]; }  
    while (depth[b] < depth[a]) { a = parent[a]; }
    while (a != b && a != -1 && b != -1) {
      a = parent[a];
      b = parent[b];
    }
    if (a == -1) return 0LL;
    return cost[a];
  };
  ll minCost = cost[leaves[0]] + cost[leaves[1]];
  
  for (int i = 0; i < leaves.size(); ++i) {
    for (int j = i+1; j < leaves.size(); ++j) {
      int a = leaves[i], b = leaves[j];
      ll costAB = cost[a] + cost[b] - lca_cost(a,b);
      minCost = min(minCost, costAB);
    }
  }
  
  cout << minCost << '\n';
}

If you found this solution helpful, consider leaving a star!